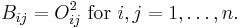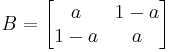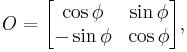Orthostochastic matrix

In mathematics, an orthostochastic matrix is a doubly stochastic matrix whose entries are the square of the absolute value of some orthogonal matrix.

The detailed definition is as follows. An square matrix B of size n is doubly stochastic (or bistochastic) if all its rows and columns sum to 1 and all its entries are nonnegative real numbers, each of whose rows and columns sums to 1. It is orthostochastic if there exists an orthogonal matrix O such that

$B_{ij}=O_{ij}^2 \text{ for } i,j=1,\dots,n. \,$

All 2-by-2 doubly stochastic matrices are orthostochastic (and also unistochastic) since for any

$B= \begin{bmatrix} a & 1-a \\ 1-a & a \end{bmatrix}$

we find the corresponding orthogonal matrix

$O = \begin{bmatrix} \cos \phi & \sin \phi \\ - \sin \phi & \cos \phi \end{bmatrix},$

with 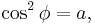$\cos^2 \phi =a,$ such that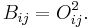 $B_{ij}=O_{ij}^2 .$

For larger n the sets of bistochastic matrices includes the set of unistochastic matrices, which includes the set of orthostochastic matrices and these inclusion relations are proper.